From the below images of Sigmoid & Tanh activation functions we can see that for the higher values(lower values) of Z (present in x axis where z = wx + b) derivative values are almost equal to zero or close to zero.

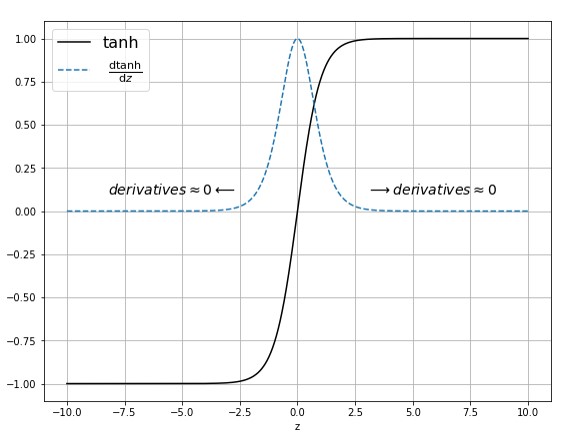
So for the higher values of Z , we will have vanishing gradients problem where network will either learn slowly or not learn at all. Value of Z also depends on the values of weights. So we can understand that weight initialization plays an important part in the performance of neural networks.Below is an another example of how initialization of weights to random normal distribution(with mean zero and standard deviation with 1) can also cause problem.

For the above example , if we assume that output from the previous layer(with 250 number of nodes) are all one and weights are initialized with a random normal distribution with mean zero and standard deviation equal to one. Then the value of Z would be just the sum of the weights(as X =1 in previous layer). What would the mean and variance of Z ? Knowing the variance or standard deviation of Z , you would be able to guess the range of values of Z.
Mean of z : Z as sum of normally distributed number with mean of zero will have a mean of zero.
What About the Variance: Variance or standard deviation of Z would be greater than 1 because each of the numbers(weights) have variance equal to one. So the variance of Z would the sum of the the variances of each numbers that would equal to (number of weights*1) i.e. 250. Which implies that standard deviation would around 15 as shown above. This will lead to very higher(or high negative) values of Z.
So we can say that by controlling or reducing the variance of Z we can control the range of values of Z.
Below are the few weight initialization algorithms we have to control the weights variance –
Normal Initialization:
As we saw above in Normal initialization variance grows with the number of inputs.
Lecun Initialization:
In Lecun initialization we make the variance of weights as 1/n.
Where n is the number of input units in the weight tensor. This initialization is the default initialization in Pytorch , that means we don’t need to any code changes to implement this. Almost works well with all activation functions.
Xavier(Glorot) Initialization:
Works better with sigmoid activations. In Xavier initialization we make the variance of weights as shown below –

Kaiming (He) Initialization:
Works better for layers with ReLU or LeakyReLU activations. In He initialization we make the variance of the weights as shown below –

Now let’s see how we can implement this weight initialization in Pytorch.
Press up/down/right/left arrow to browse the below notebook.
Reference:
https://www.deeplearningwizard.com/deep_learning/boosting_models_pytorch/weight_initialization_activation_functions/#zero-initialization-set-all-weights-to-0
Do like , share and comment if you have any questions.
