In the last post we discussed two approaches to fine tuning using feature-based method, these options may not be always efficient in terms of computational complexity as well as time complexity. Full fine tuning of any LLM models needs to stitch the below mentioned steps together:
- Load dataset in memory
- Load pretrained model in the memory
- Foward pass through the network
- Loss calculation and gradient calculations
- Optimize the weights
Combination of all these steps can produce lot of challenges in terms of –
- Memory requirements
- Computational requirements like more GPU
- Training time and associated cost
- Inference time
In one of the paper published by Microsoft, it has been shown that there exists a way called Parameter Efficient fine tuning which can help to tackle the above-mentioned problems. In this paper a technique called LoRA (Low Rank Adoption) has been introduced. In principle the concept resolves around the concept of Matrix Decomposition in lower ranks. A full fine-tuning of LLM goes through mainly two separate steps to generate the embeddings – 1. Foward pass through the network 2. Weights updates and in the end get the final embeddings as shown below –

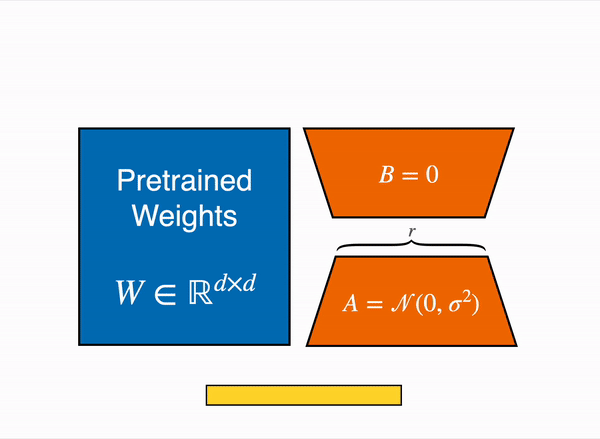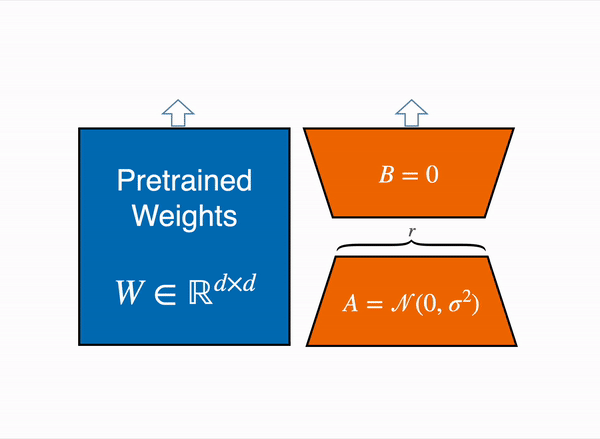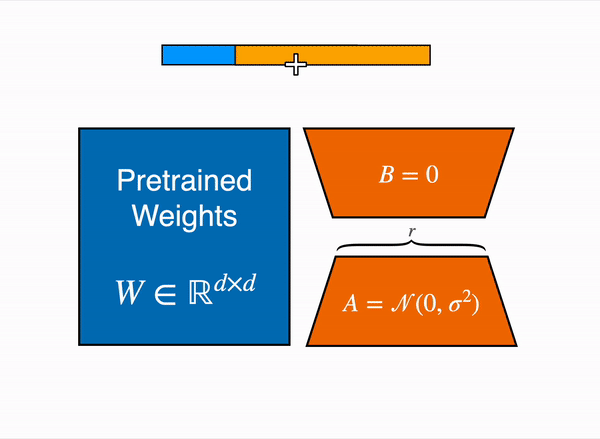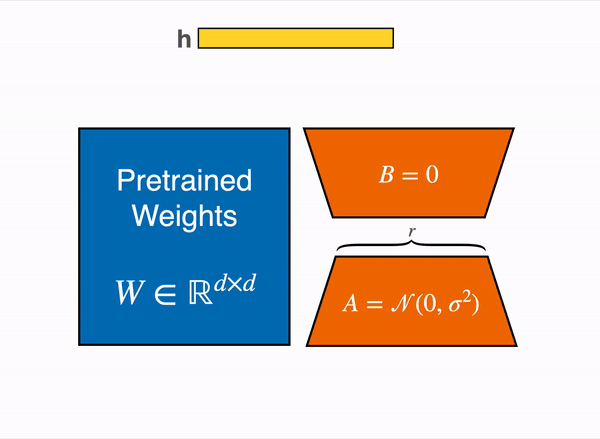
In case of LoRA it has been shown that pretrained model has low intrinsic dimensions, in other words there exists a low dimension reparameterization that is as effective doing the full parameter fine tuning. Pretrained weights can decomposed in low rank (Rank is linearly independently rows or columns of a matrix) matrices as shown below-

For examples imagine that W is the pre trained weights with the dimension of 512 X 64. So we can say that if we want to full finetune the weights that total number of parameters would be 512 X 64 = 32768 which is lot of parameters to train. However, if we use two low rank matrices where the rank is 4 then these two matrices A and B can be represented (low dimension reparameterization) as follows
– A – 4 X 64 and B – 512 X 4.
So the total numbers of parameters would be (4 x 64 + 512 x 4) = 2304 which lot less when we compared to approximately 32k parameters. During training time, we freeze the pre-trained model parameters frozen and only train these two low rank matrices. During inference we combine these two matrices and add back to the pre-trained model weights as shown below –
We can also train these low rank metrices for specific tasks and during inference time we can add back the task specific LoRA weights to the pretrained weights as shown below –
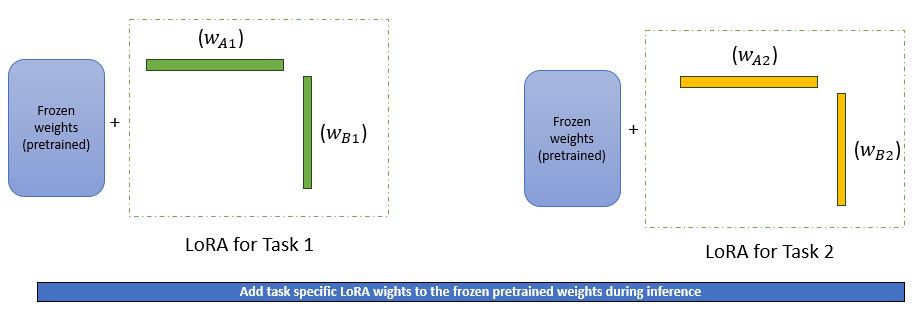
In the previously mentioned paper it has been shown that similar model performence like full fine tuning can be achieved with LoRA as shown below –
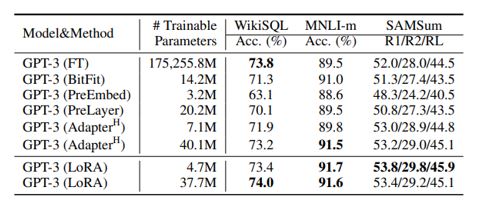
In the LoRA they used the low rank adoption for different attention weight matrices like Q ,V. The study in the paper has been limited to only adapting the attention weights for downstream tasks and freeze the MLP modules (so they are not trained in downstream tasks) both for simplicity and parameter-efficiency. Surprisingly it has been observed that with low rank as low as r=1 very good performance can be achieved (r is hyperparameter to tune).

In the next blog post we will implement the LoRA in code. Do like, share the post in case you find this post useful. Thanks for reading.
