In the previous post we talked about the basics of Graphs , adjacency matrix and why representation of Graph data and using the same for Machine Learning tasks are different than other forms of data. In this post I will try to explain the very basic Message Passing technique used in Graph Neural Networks. In one of the previous blog post I talked about why we need to use Convolutional neural network instead of Multilayer perceptron in case of images , to solve the graph neural network problems almost the same concept of convolution (Graph convolution network) has been used , which we will discuss in detail in here.
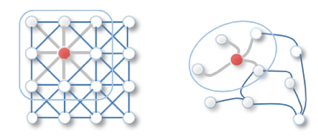
CNN is computationally challenging and expensive to perform on graph data because the graph topology is very arbitrary and with complications, also there is no spatial locality in case of graphs. Additionally, there is an unfixed node ordering, which complicates the use of CNN.
As we can see above in case of CNN we run through a trainable filter or kernel across the image to extract features in case of Graphs , almost similar technique called message passing is being used which generally works on the principle of ‘a node one edge away is more likely to to be inter related rather than a node which is four or five edges away’. The main aim of the message passing technique is to come up with a optimal node embedding iteratively which captures the context and neighborhood information. Message passing technique has two steps – 1. Aggregation 2. Update as shown in the below image.
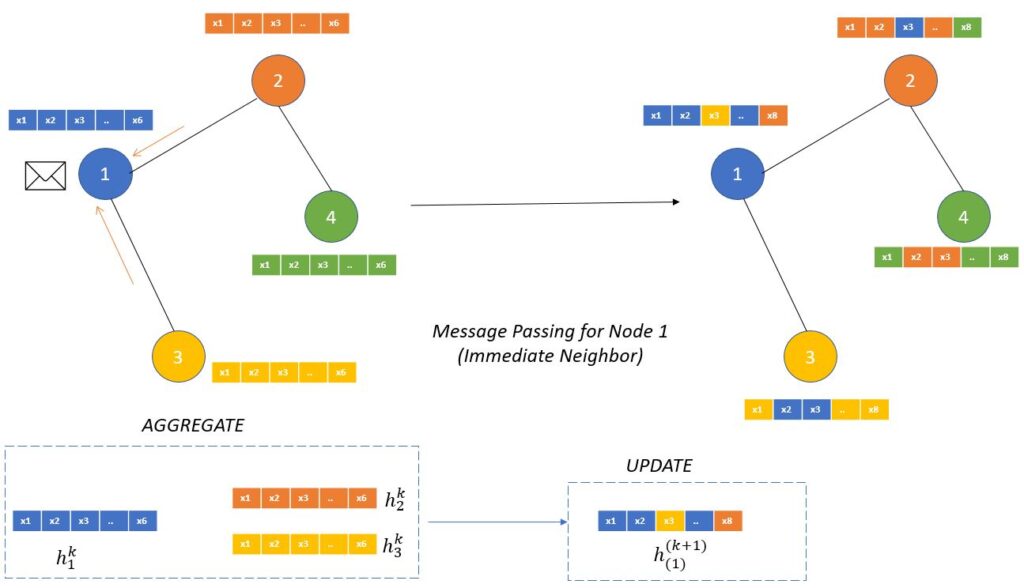
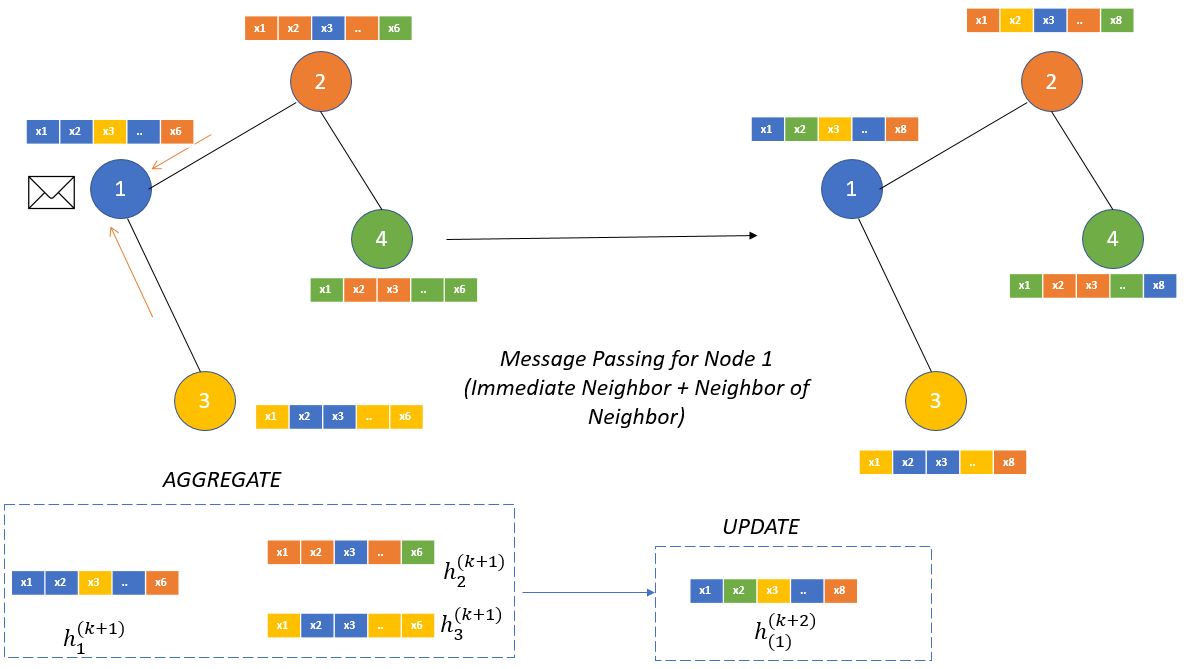
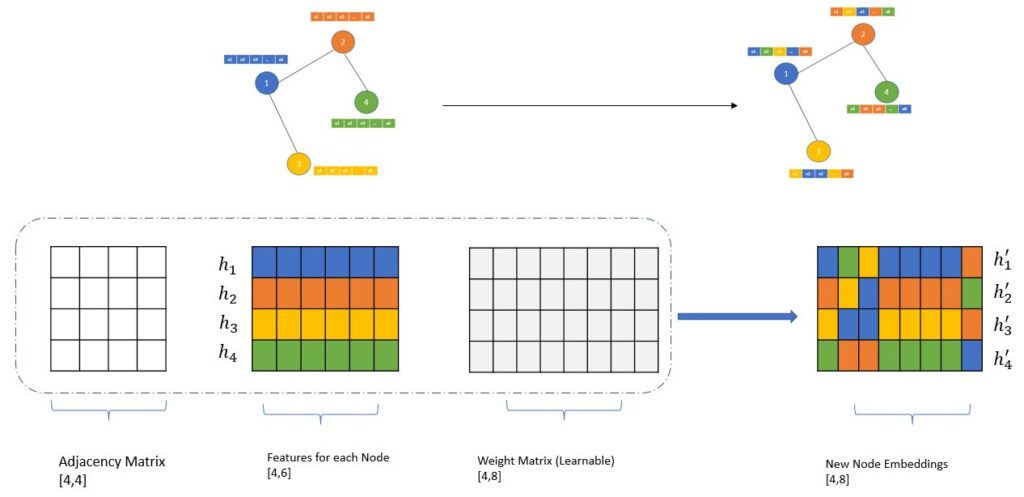
To understand the message passing technique , suppose we have a graph with four nodes which are having six dimensional feature and denoted with different colors and we are only concentrating on the node 1. As mentioned earlier message passing technique will first aggregate the features for it’s immediate neighbors (using adjacency matrix). Once the aggregation is done then it will update it’s own state.
- This aggregate function should be a permutation invariance function like sum or average
- The update function itself can be a neural network (with attention or without attention mechanism) which will generate the updated node embeddings.
At time-stamp k we can see that node 1 has only its own features , however after aggregation/update operation it captures the features or the qualities of its immediate neighbors (node 2 and 3) which is shown in the (k+1) step. Node 1 color has changes from all blue to blue along with yellow and orange , however node 1 still doesn’t have the message from node 4 which is green in color. Green message is only propagated to node 2. You should also notice that embedding size has been changed in (k+1) which is again a hyperparameter.
Let’s see what will happen if we do another round of neighborhood hopping.
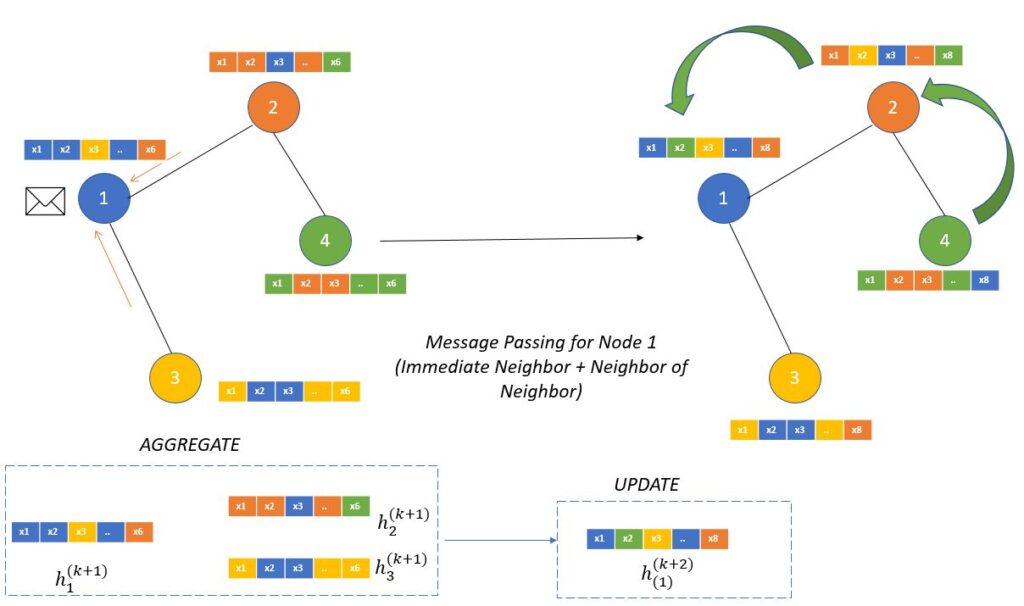
With this round of neighborhood hoping we can see that properties of node 4 in green has been passed through to node 1 via node 2 in (k+2)th iteration. This is the essence of message passing we can pass message from surrounding nodes to every other nodes in the graph. Number of hoping is a sensitive parameter which cause overfitting or over smoothing of information for large graphs.
In case of CNN the filter or the kernel weights are the learnable parameters, here in case of GNN or GCN a learnable matrix is present whose weights are optimized during the update phase using neural network as mentioned earlier. Adjacency matrix is also used to fetch the neighborhood information as shown below to come with the new set of embedding for each of the nodes. Embedding size is again a hypermeter which should be tuned during the training phase.
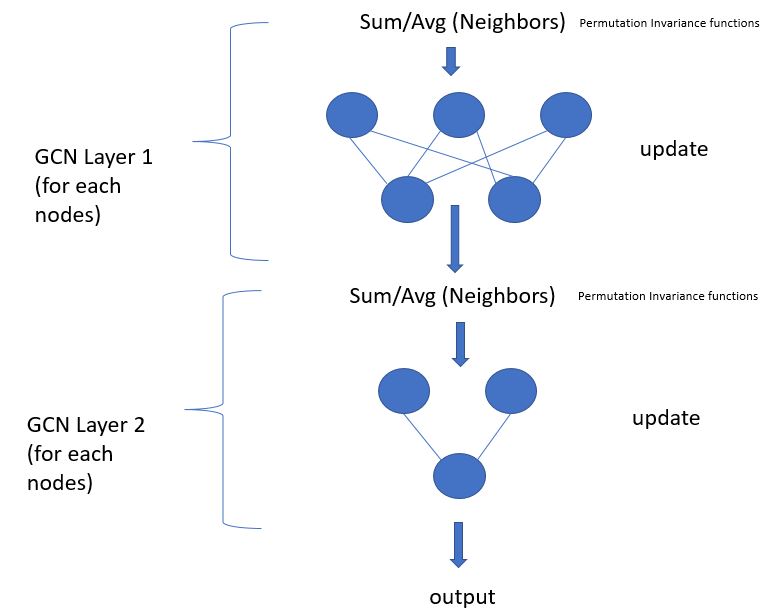
Neighborhood hoping is nothing but stacking multiple GCN layer on top of each other as shown below, output size can be varied according to the requirement, in the below example one node is present at the output which is similar to doing node label binary classification.
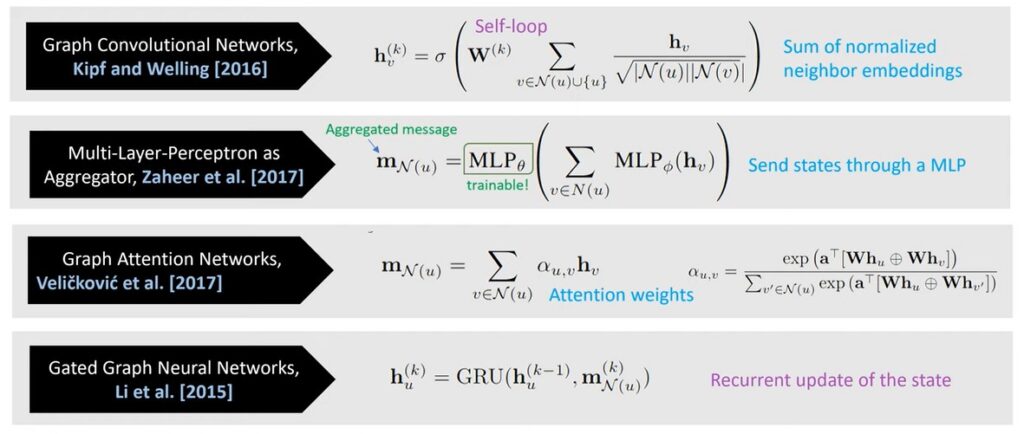
Based on the aggregate and update function we can have different types of Graph Neural Networks as shown below –
Thanks for reading, hope you got some idea of the inner working of GNN, in the next tutorial we will do code implementation using pytorch geometric.
Do comment if you have any questions.